Implementation of HLLD Riemann solver in PIERNIK
Varadarajan Parthasarathy1, Artur Gawryszczak1, Michal Hanasz2
1Nicolaus Copernicus Astronomical Centre of the Polish Academy of Sciences
2Toruń Centre for Astronomy Nicolaus Copernicus University
2Toruń Centre for Astronomy Nicolaus Copernicus University
PIERNIK is a freely available, massively parallel, multi-fluid, multi-grid, magnetohydrodynamical (MHD) code. We have implemented the multi-state Harten-Lax-van Leer approximate Riemann solver for ideal magnetohydrodynamics - HLLD (”D” denotes Discontinuities) in PIERNIK. Our goal is to perform numerical simulations of hypersonic astrophysical flows in 1, 2 and 3 spatial dimensions, particularly in the presence of discontinuities, using the HLLD Riemann solver. The HLLD Riemann solver is more robust than the linearized Riemann solver, capable of resolving isolated discontinuities formed in the MHD system (hence named as HLLD) and corresponds to the HLLC (”C” denotes Contact) Riemann solver when the magnetic field vanishes. We demonstrate the robustness and accuracy of the HLLD Riemann solver implemented in PIERNIK through numerical tests and several interesting features available in the PIERNIK
Keywords: Computational methods, Magnetohydrodynamics, Turbulence
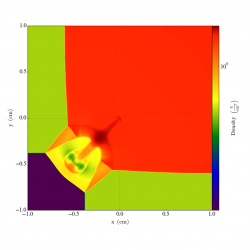
Figure 1:
2D Riemann problem: Domain: [(-1,1), (-1,1)], Resolution: [512,512]. Log plot of mass density at \(t = 9\)